игры.su -
купить или арендовать доменное имя онлайн- Домены совпадающие с игры
- Покупка
- Аренда
- игры.su
- договорная
- договорная
- Домены начинающиеся с игры
- Покупка
- Аренда
- игры24.рф
- 220 000
- 2 200
- Домены с синонимами игры
- Покупка
- Аренда
- videoigra.ru
- 50 000
- 500
- игровые.рф
- 70 000
- 700
- Домены с переводом игры
- Покупка
- Аренда
- audioplayers.ru
- 50 000
- 500
- Плейбокс.рф
- 150 000
- 1 500
- плейер.рф
- 550 000
- 5 500
- плейеры.рф
- 550 000
- 5 500
- плэер.рф
- 100 000
- 1 000
- Домены содержащие игры
- Покупка
- Аренда
- Проигрыватели.рф
- 150 000
- 1 500
- развивающиеигры.рф
- 88 000
- 880
- флэшигры.рф
- 110 000
- 1 100
- Домены с синонимами, содержащими игры
- Покупка
- Аренда
- vosproizvedenie.ru
- 50 000
- 500
- поиграй.рф
- 70 000
- 700
- поиграть.рф
- 100 000
- 1 000
- Проиграть.рф
- 70 000
- 700
- Домены с переводом, содержащими игры
- Покупка
- Аренда
- seksigry.ru
- 50 000
- 500
- опля.рф
- 50 000
- 500
- Плебей.рф
- 70 000
- 700
- Плены.рф
- 70 000
- 700
- плиты.рф
- 350 000
- 3 500
- Пловы.рф
- 70 000
- 700
- плоты.рф
- 150 000
- 1 500
- Плуты.рф
- 70 000
- 700
- плясы.рф
- 100 000
- 1 000
- Проплаты.рф
- 150 000
- 1 500
- Аренда или покупка домена экзаменаторы.рф: Выгода и преимущества для вашего бизнеса
- Расширьте свои возможности онлайн-преподавания и повысьте узнаваемость бренда, приобретая или арендуя доменное имя экзаменаторы.рф для целевой аудитории России.
- Эксклюзивный домен щ1.рф: Почему он станет визитной карточкой вашего бизнеса
- Погрузитесь в цифровой мир России с доменным именем щ1.рф – идеальным выбором для создания узнаваемого онлайн-бренда и обеспечения эффективного продвижения вашего бизнеса в регионе.
- Шуточка.рф: Твоя Личная Смехотерапия в Сети - Аренда или Покупка Домена
- Узнайте, как купить или арендовать доменное имя 'шуточки.рф' для добавления юмора и уникальности вашему онлайн-представлению.
- Почему выбирают доменное имя шулеры.рф: безопасность и преимущества
- Ознакомьтесь с преимуществами обладания или аренды доменного имени 'шулеры.рф' для защиты репутации, улучшения позиций в поисковых системах и укрепления имённого бренда в Рунете.
- Штиблета.рф: Почему выгодно купить или арендовать доменное имя для вашего бизнеса
- Узнайте, почему обладание или аренда уникального доменного имени штиблета.рф - это стратегический шаг для улучшения связи с российскими потребителями и укрепления вашего онлайн-присутствия.
- Школьные технологии и успешные учреждения: почему ШКП.РФ - выбор для комфортной аренды или покупки домена
- Узнайте, почему приобретение или аренда доменного имени ШКП.РФ является стратегическим решением для укрепления онлайн-присутствия и доверия клиентов в Российском сегменте Интернета, гарантируя быструю идентификацию вашего бизнеса и доступ к обширной аудит
- Доменное имя для школьников: зачем арендовать или купить schoolar.ru
- Узнайте, как покупка или аренда доменного имени 'школяра.рф' может повысить доверие к вашему образовательному проекту и обеспечить стабильность в интернете.
- Шедеврики.рф: Почему Вам стоит купить или арендовать это доменное имя
- Оптимизируйте свою онлайн-присутствие с шедеврыки.рф – уникальным и запоминающимся доменным именем, обеспечивающим креативность, запоминаемость и расширенную возможность продвижения в российском сегменте интернета.
- Почему выбирая доменное имя шашлычок.рф, вы идете по правильному пути к успеху
- Публичная интернет-площадка статьи на сайте 'Шашлычок.рф' - ваш ключ к успеху в отрасли шашлычной вкусностей, стимулирующий как продажи, так и образ бренда среди человека, который любит быть в курсе текущих трендов оборудования для шашлыков.
- Доменное имя шахматист.рф: Собственное или арендованное - путь к успеху для шахматистов
- Не пропустите возможность приобрести или арендовать уникальное доменное имя шахматист.рф и стимулировать свой бизнес в мире шахмат, обеспечив легкое запоминание имени вашего сайта и доверие посетителей.
- Экспорт на новый уровень с “экспортирование.рф”: идеальный домен для развития бизнеса
- Поднимите экспорт на новый уровень с доменом “.рф”, где “экспортирование.рф” - ваш идеальный выбор для успешного продвижения продукции на международный рынок и укрепления российского бренда.
- Эйфория.рф: Выбор идеального доменного имени для бизнеса — покупка или аренда
- Ознакомьтесь с преимуществами покупки или аренды лучшего доменного имени для вашего бизнеса на Эйфория.рф, чтобы улучшить эффективную продвижение и увеличить прибыль на цифровом рынке.
- Аренда и Покупка ДОМЕНа ЭГБ.РФ: Ваша Стратегия Выживания в Интернет Войнах
- Узнайте, как аренда и покупка домена .ЭГБ.РФ оптимизируют ваш бизнес, укрепляя интернет-присутствие и гарантируя уважение профессионального сообщества.
- Эволюционное лидерство с EvgenyLikhoded.com: Формирование сильного онлайн-имиджа для укрепления лидерской позиции в бизнесе
- Ознакомьтесь с эволюционным лидерством на EvgenyLikhoded.com и научитесь создавать эффективный онлайн-идентификатор для поддержания лидерства в современном бизнесе.
- Щенка.рф: Создание веб-сайта про щенков и собак - доменное имя для покупки и аренды
- Создайте свой уникальный сайт о щенках и собаках с помощью доменного имени Щенка.рф, либо купив его, либо арендуя на выгодных условиях - ваш питомец заслуживает лучшего представления в Интернете.
- Инвестируйте в юмор России: аренда или покупка доменного имени шутихи.рф
- Ознакомьтесь со стратегиями инвестирования в распространение юмора в России, исследуя потенциал доменного имени шутихи.рф при аренде или покупке, чтобы продемонстрировать бизнесу и отдельным лицам климатические возможности цифровой комедии в интернете.
- Купить или арендовать доменное имя .рф: Выгоды и Преимущества для Вашего Интернет-Проекта
- Узнайте, где и как купить или арендовать уникальное доменное имя шурф.рф для вашего интернет-проекта, максимизируя прибыль и получая отличные преимущества, чтобы выделиться в Интернете.
- Штукатурик.рф: Эволюция Онлайн-Статуса - Покорение Цифрового Неба
- Узнайте секреты повышения онлайн-статуса и гарантированного успеха с помощью Штукатурик.рф - ваш надежный помощник на пути к достижению целей в интернете!
- Штрафик.рф: Аренда или Покупка Домена - Ключ к Эффективному Онлайн-Развитию
- Узнайте, насколько важны аренда или покупка домена для успешного онлайн-развития с помощью надежного эксперта в области доменных услуг - Штрафик.рф.
- Аренда или Покупка Доменного Имена ШТА.РФ: Русский Путь в Интернет-Бизнесе
- Откройте двери российского интернет-рынка с арендой или покупкой доменного имени на домене .РФ, гарантируя потенциальным клиентам узнаваемость и локальную поддержку вашего бренда в сети ШТА.РФ!
- Шлягеры.рф: Пошаговая стратегия построения успешного онлайн-бизнеса в музыкальной индустрии
- Изучаем стратегии и секреты создания прибыльного онлайн-платформы для музыкальных хитов на примере Шлягеры.рф, где любители мелодий и независимые исполнители находят среду для взаимовыгодного сотрудничества и раскрутки творчества в музыкальной индустрии.
- Успешный сайт для вашей школы с доменом школа24.рф: инвестиции в будущее образования
- Создайте успешный онлайн-портал для вашей школы с доменом школа24.рф и вкладывайтесь в будущее образования, обеспечивая учащимся лучшие условия для обучения и развития.
- Доменное имя шифровальщики.рф: Легендарные секреты безопасности для вашего выдающегося бизнеса
- Сокройте свои секреты и усилите безопасность бизнеса с доменным именем шифровальщики.рф — идеальным выбором для тех, кто ценит конфиденциальность и стабильность в онлайн-мире.
- Шелл.рф – Ваш проход к успеху в интернет пространстве для аренды или покупки доменного имени сегодня
- Шелл.рф – Ваш Вратарь в Световые Поиски, предлагаем уникальные домены для невероятного успеха в Интернете, в вашем распоряжении охотное место и подборка вне конкуренции для покупки или аренды штампа коллекционных доменов прямо сейчас.
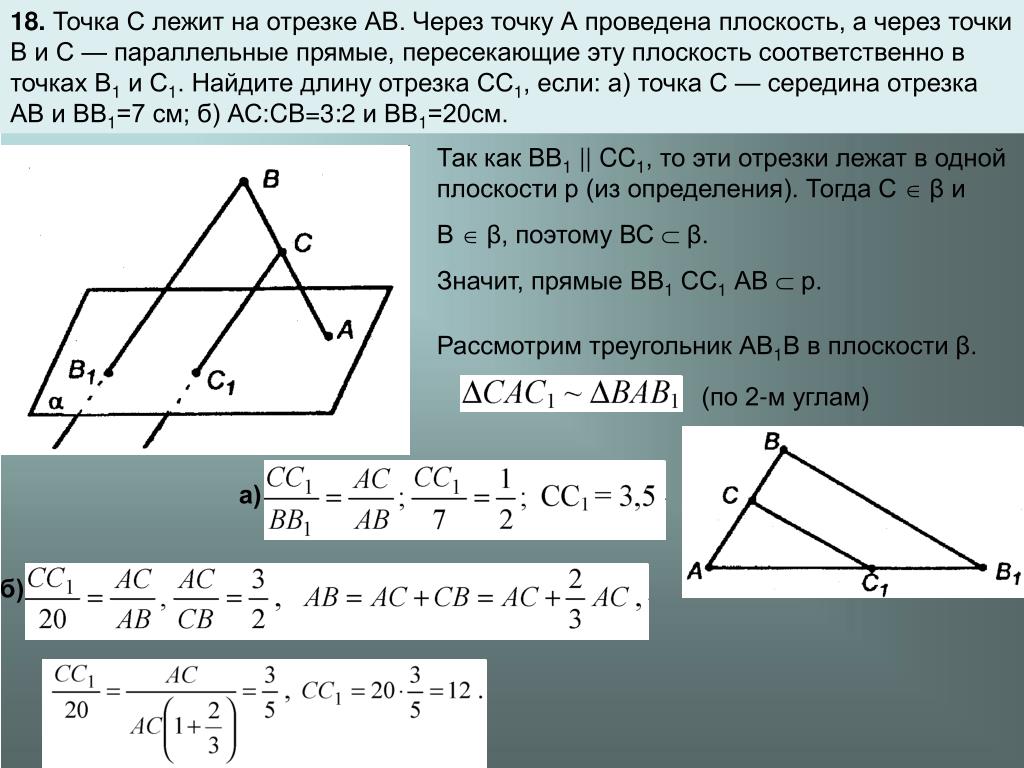
Точка расположена на отрезке, плоскость проходит через нее и параллельна двум данным прямым
Для начала, рассмотрим что такое точка с на отрезке ав. Это означает, что данная точка с лежит на отрезке, соединяющем две заданные точки а и в. Точка с находится между точками а и в и делит отрезок ав на две части в определенном отношении. Чтобы определить положение точки с на отрезке ав, мы можем использовать формулу нахождения координат точки по формуле с = (а + в)/2. Здесь а и в - координаты заданных точек, а с - координаты искомой точки с. Когда мы рассмотрим построение параллельных прямых в плоскости а через точки а и с, мы должны помнить о следующем. Для конструирования параллельной прямой, достаточно найти ее уравнение и использовать его для построения данной прямой. В данном случае мы знаем координаты точек а и с, и можем использовать эти данные для нахождения уравнения параллельной прямой. Что такое точка с на отрезке ав?Точка С на отрезке АВ играет важную роль в геометрии и математике в целом. Она позволяет решать различные задачи, связанные с расположением точек и отрезков в пространстве. Кроме того, точка С на отрезке АВ может использоваться для построения параллельных прямых в плоскости А, проходящих через точки А и С. Это свойство точки С помогает решать задачи по определению и построению параллельных линий и поверхностей.
Основные понятия и определенияПеред тем, как перейти к изучению точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с, полезно разобраться в некоторых основных понятиях.
Знание этих основных понятий и определений поможет нам лучше понять тему точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с и успешно продолжить изучение данной темы. Как найти точку с на отрезке ав?Чтобы найти точку С на отрезке АВ, нам понадобятся координаты точек А и В. Представим отрезок АВ в виде прямой, проходящей через эти две точки. Для нахождения точки С, которая будет лежать на этой прямой и параллельна другой прямой в плоскости А, используем формулу: С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) Здесь t – параметр, принадлежащий отрезку [0, 1]. Если t = 0, то точка С будет совпадать с точкой А, если t = 1 – с точкой В. Итак, мы знаем координаты точек А и В, а также значения параметра t. Подставляем все это в формулу и получаем координаты точки С. Пример:
Пусть А(2, 3) и В(6, 9). Находим значений параметра t, например, t = 0.5. С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) С(xС, yС) = (2, 3) + 0.5 * ((6, 9) - (2, 3)) С(xС, yС) = (2, 3) + 0.5 * (4, 6) С(xС, yС) = (2, 3) + (2, 3) С(xС, yС) = (4, 6) Таким образом, точка С находится на середине отрезка АВ и имеет координаты (4, 6). Существование и уникальность точки CДля того чтобы точка C существовала на отрезке AB и была параллельна прямым в плоскости, проходящим через точки A и B, необходимо выполнение определенных условий. Во-первых, для существования точки C на отрезке AB необходимо, чтобы точка A не совпадала с точкой B, иначе отрезок будет вырожденным. Во-вторых, чтобы точка C была параллельна прямым, нужно убедиться, что отрезок AB и прямые в плоскости, проходящие через точки A и B, действительно параллельны. Это означает, что угол между отрезком AB и любой из этих прямых должен быть равен 180 градусам. Если все условия выполнены, то точка C существует и является уникальной на отрезке AB, параллельна прямым в плоскости, проходящим через точки A и B. Параллельные прямые в плоскости а
Если две прямые параллельны, то их наклоны равны. Наклон прямой определяется через разность координат точек, через которые проходит прямая. Например, если прямая проходит через точки (х1, у1) и (х2, у2), то наклон прямой равен: м = (у2 - у1) / (х2 - х1). Если наклоны двух прямых равны, то они параллельны. И наоборот, если две прямые параллельны, то их наклоны равны. Кроме определения параллельности через наклоны прямых, можно использовать еще один способ - построение плоскости а. Для этого необходимо провести прямую через две точки a и с, а затем, провести скрещивающую прямую через точку a, параллельную прямой о. Если эти две прямые не пересекаются, то прямая о и параллельна прямой в плоскости а.
Уравнения прямых о и а имеют одинаковую функцию (2х), поэтому их наклоны равны и они параллельны. Как найти параллельные прямые через точки а и с?Для того чтобы найти параллельные прямые, проходящие через заданные точки A и C на плоскости, необходимо выполнить следующие шаги: Шаг 1: Определите координаты точек A и C. Для этого вам понадобятся значения x и y для каждой из точек. Шаг 2: Определите уравнение прямой, проходящей через точку A. Для этого можно использовать формулу наклона прямой, которая выглядит следующим образом: y - y1 = m(x - x1), где m - наклон прямой, а (x1, y1) - координаты точки A. Шаг 3: Используя полученное уравнение, подставьте координаты точки C и решите полученное уравнение относительно переменной m. Таким образом, вы сможете определить наклон параллельной прямой. Шаг 4: Найдите уравнение параллельной прямой, проходящей через точку C, используя найденный наклон m и координаты точки C. Вы можете использовать формулу y - y1 = m(x - x1), где (x1, y1) - координаты точки C. Шаг 5: Проверьте полученное уравнение, подставив в него координаты точек A и C. Если оба значения равны, значит, прямая, построенная по уравнению, параллельна прямой, проходящей через заданные точки A и C. Таким образом, следуя этим шагам, вы сможете найти параллельные прямые, проходящие через заданные точки A и C на плоскости. Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ. Точка с на отрезке ав и параллельные прямые в плоскости а через точки а и с Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ.
|

 Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.
Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.